QuickTime 3 Reference

General Convolution Filter (`genk')

This effect applies a general purpose convolution effect to a single source. The effect that results is completely determined by the values entered into the kernel parameters of the effect. The kernel for this convolution is always a 3-by-3 matrix of values.

The values of the cells of the convolution kernel determine the value that is assigned to each pixel of the destination frame. The convolution algorithm examines every pixel of the source, and the eight pixels surrounding it. These values are multiplied by the appropriate values in the cells and summed. This sum is then used as the value of the corresponding destination pixel.

Many computer graphics textbooks offer a more complete and rigorous explanation of convolution, and you are encouraged to consult these for useful values that the kernel can take. A great introduction to convolution for programmers can be found in High Performance Computer Imaging, Chapter 6, by Ihtisham Kabir, Manning Publications, 1996. ISBN 1-884777-26-0. A somewhat more classical reference is: Foley J.D., van Dam A., Feiner S.K. and Hughes J.F., Computer Graphics: Principles and Practice, 2nd. Edition, pp. 629-636, Addison-Wesley, 1990. ISBN 0-201-12110-7

As an example of a kernel that produces a useful result, the following kernel values will shift an image left by one pixel:

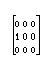
The General Convolution Filer effect takes a maximum of one sources and has nine parameters.

Parameters

Name	Code	Type	Description
Cell One	`cel1'	Fixed	The value to be placed into the first cell of the kernel.
Cell Two	`cel2'	Fixed	The value to be placed into the second cell of the kernel.
Cell Three	`cel3'	Fixed	The value to be placed into the third cell of the kernel.
Cell Four	`cel4'	Fixed	The value to be placed into the fourth cell of the kernel.
Cell Five	`cel5'	Fixed	The value to be placed into the fifth cell of the kernel.
Cell Six	`cel6'	Fixed	The value to be placed into the sixth cell of the kernel.
Cell Seven	`cel7'	Fixed	The value to be placed into the seventh cell of the kernel.
Cell Eight	`cel8'	Fixed	The value to be placed into the eighth cell of the kernel.
Cell Nine	`cel9'	Fixed	The value to be placed into the ninth cell of the kernel.

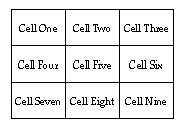
The nine cells in the kernel are laid out as follows: